图解中心化、标准化对回归的影响

数值模拟：图解中心化和标准化对系数估计的影响, 一元

中心化的影响

数值模拟

x1 <- rnorm(50,4,2)
e <- rnorm(50,0,0.1)
y <- -2 + x1 + e

x1.c <- scale(x1,scale=F)  # 中心化
y.c <- scale(y,scale=F)

回归拟合

m1 <- lm(y~x1)        # 原始回归模型, 带截距项
m2 <- lm(y~x1.c)      # x 中心化后的回归模型, 带截距项
m3 <- lm(y.c~x1)      # y 中心化后的回归模型, 带截距项
m4 <- lm(y.c~x1.c)    # x 和 y 均中心化后的回归模型, 带截距项
m5 <- lm(y~0+x1.c)    # x 中心化后的回归模型, 不带截距项
m6 <- lm(y.c~0+x1)    # y 中心化后的回归模型, 不带截距项
m7 <- lm(y.c~0+x1.c)  # x 和 y 均中心化后的回归模型, 不带截距项

图解

中心化带截距项

plot(x1, y, xlab="x", ylab="y", ylim=c(-8,8), xlim=c(-8,8), pch=15)    # 绘制散点图
abline(h=0, v=0, lty=2)
abline(reg=m1, col="black", lwd=2)                # 原始回归模型

points(x1.c, y, col="blue", pch=17)               # x 中心化后的数据
abline(reg=m2, col="blue", lwd=2)                 # x 中心化后的回归模型, 带截距项

points(x1, y.c, col="red", pch=19)                # y 中心化后的数据
abline(reg=m3, col="red", lwd=2)                  # y 中心化后的回归模型, 带截距项

points(x1.c, y.c, col="yellow", pch=21)           # x 和 y 均中心化后的数据
abline(reg=m4, col="yellow", lwd=2)               # x 和 y 均中心化后的回归模型, 带截距项

image-20221124151118199

X中心化不带截距项

plot(x1, y, xlab="x", ylab="y", ylim=c(-8,8), xlim=c(-8,8), pch=15)    # 绘制散点图
abline(h=0, v=0, lty=2)
abline(reg=m1, col="black", lwd=2)                # 原始回归模型

points(x1.c, y, col="blue", pch=17)               # x 中心化后的数据
abline(reg=m5, col="blue", lwd=2)                 # x 中心化后的回归模型, 不带截距项
legend("topleft",inset = 0.04,c('m1','m6'),pch = c(15,17),col = c("black","blue"))

image-20221124151348892

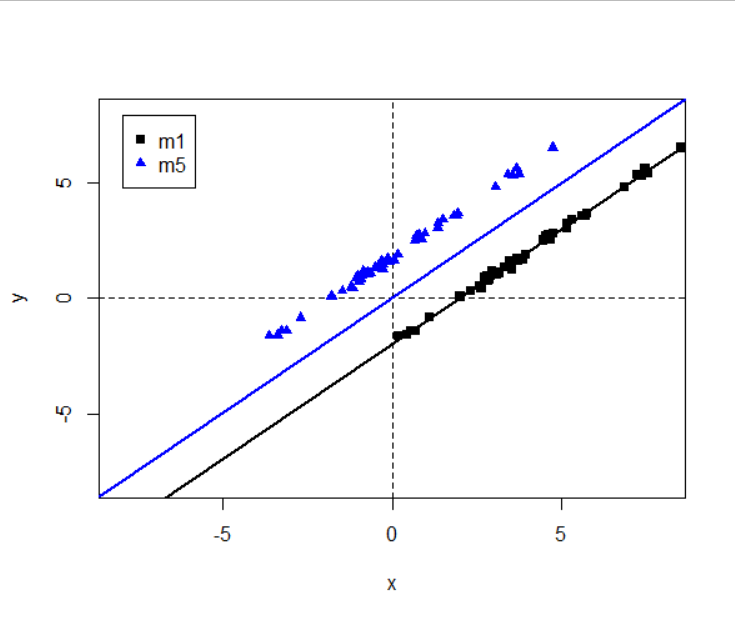
Y中心化不带截距项

plot(x1, y, xlab="x", ylab="y", ylim=c(-8,8), xlim=c(-8,8), pch=15)    # 绘制散点图
abline(h=0, v=0, lty=2)
abline(reg=m1, col="black", lwd=2)                # 原始回归模型
points(x1, y.c, col="red", pch=19)                # y 中心化后的数据
abline(reg=m6, col="red", lwd=2)                  # y 中心化后的回归模型, 不带截距项
legend("topleft",inset = 0.04,c('m1','m6'),pch = c(15,19),col = c("black","red"))

image-20221124151832107

X中心化、Y中心化不带截距项

## 中心化对回归的影响 ##
plot(x1, y, xlab="x", ylab="y", ylim=c(-8,8), xlim=c(-8,8), pch=15)    # 绘制散点图
abline(h=0, v=0, lty=2)
abline(reg=m1, col="black", lwd=2)                # 原始回归模型
points(x1.c, y.c, col="yellow", pch=21)           # x 和 y 均中心化后的数据
abline(reg=m7, col="yellow", lwd=2)               # x 和 y 均中心化后的回归模型, 带截距项
legend("topleft",inset = 0.04,c('m1','m7'),pch = c(15,21),col = c("black","yellow"))

image-20221124151941300

m2与m4的关系：将m2平移至过原点, 即得m4

m3 m4 m5得到相同的拟合直线, 但m4与m3 m5对应的响应变量不同, 是针对不同数据得到的拟合直线.

事实上, 当y的均值离0较远时, m6得到的拟合直线的效果往往较差,

这是因为假定的模型(不含截距项)与真实的模型(含有截距项)相差较远.

标准化带截距项

plot(x1, y, xlab="x", ylab="y", ylim=c(-8,8), xlim=c(-8,8), pch=15)    # 绘制散点图
abline(h=0, v=0, lty=2)
abline(reg=n1, col="black", lwd=2)                # 原始回归模型

points(x1.s, y, col="blue", pch=17)               # x 中心标准化后的数据
abline(reg=n2, col="blue", lwd=2)                 # x 中心标准化后的回归模型, 带截距项

points(x1.s, y.s, col="red", pch=19)              # x 和 y 均中心标准化后的数据
abline(reg=n3, col="red", lwd=2)                  # x 和 y 均中心标准化后的回归模型, 带截距项
legend("topleft",inset = 0.04,c('n1','n2','n3'),pch = c(15,17,19),col = c("black","blue","red"))

image-20221124152505744

标准化不带截距项

plot(x1, y, xlab="x", ylab="y", ylim=c(-8,8), xlim=c(-8,8), pch=15)    # 绘制散点图
abline(h=0, v=0, lty=2)
abline(reg=n1, col="black", lwd=2)                # 原始回归模型

points(x1.s, y, col="blue", pch=17)               # x 中心标准化后的数据
abline(reg=n4, col="blue", lwd=2)                 # x 中心标准化后的回归模型, 带截距项

points(x1.s, y.s, col="red", pch=19)              # x 和 y 均中心标准化后的数据
abline(reg=n5, col="red", lwd=2)                  # x 和 y 均中心标准化后的回归模型, 带截距项
legend("topleft",inset = 0.04,c('n1','n4','n5'),pch = c(15,17,19),col = c("black","blue","red"))

image-20221124152717695

n2与n4的关系：将n2平移至过原点, 即得n4

n3 n5得到相同的拟合直线