回归分析

R语言回归分析相关流程

数据预处理

• 中心化标准化

  data <- as.data.frame(scale(data, center = T, scale = T))    # 标准化
  data <- as.data.frame(scale(data, center = T, scale = F))    # 中心化

变量相关性检验

• 使用Hmisc

  library(Hmisc)
  rcorr(as.matrix(data), type = 'pearson')
  R <- rcorr(as.matrix(data), type = 'pearson')$r  # 相关系数阵
  P <- rcorr(as.matrix(data), type = 'pearson')$P  # 相关性检验的P值

• 使用psych

  library(psych)
  corr.test(data,use="complete")

• 热力图

  library(Hmisc)
  R <- rcorr(as.matrix(data), type = 'pearson')$r # 相关阵
  library(corrplot)
  corrplot(R, method="color", addCoef.col='grey', tl.col='black') # 热力图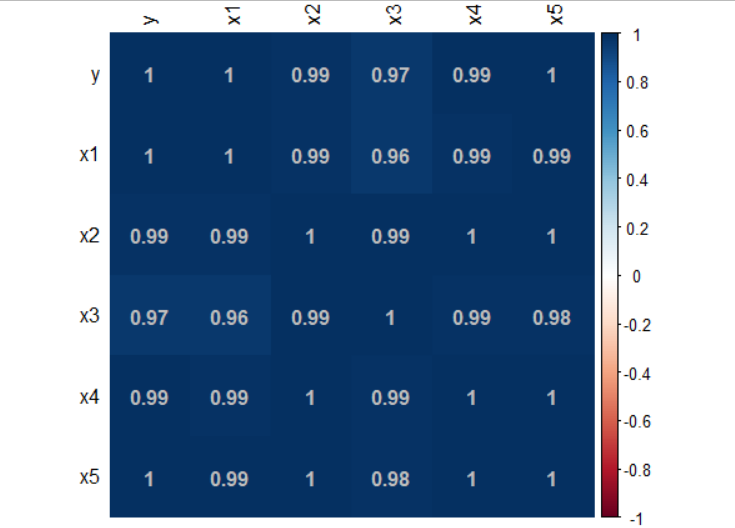

  

  image-20221124123849236
• 使用ggplot绘制热图

  library(Hmisc)
  R <- rcorr(as.matrix(data), type = 'pearson')$r # 相关阵
  library(reshape2)  
  melted_r <- melt(R)  # 将相关系数矩阵拉直
  library(ggplot2)
  ggplot(data = melted_r, aes(x=Var1,y=Var2,fill = value)) + # ggplot2 基本图层
    geom_raster() + # 绘制热力图
    scale_fill_gradient2(low = rgb(10,8,32,max = 255),mid = rgb(165,24,90,max = 255),
                         high = rgb(249,228,209,max = 255),limit = c(0,1),
                         name="Pearson\nCorrelation") + 
    theme( # 调整图表样式
      axis.title = element_blank(), # 删除ggplot2的坐标标签
      panel.background = element_blank(), # 删除ggplot2的灰色背景
      panel.grid.major = element_blank(), # 删除ggplot2的面板网格
      panel.border = element_blank(),
      axis.ticks = element_blank() # 删除ggplot2的轴刻度
    ) + 
    geom_text(aes(Var2,Var1,label = round(value,2)),
              color = '#228B22',size = 2) # 加上相关系数数值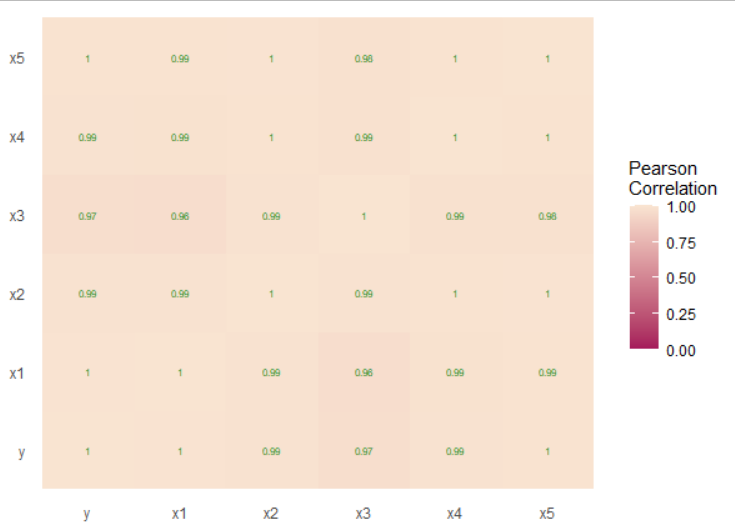

  

  image-20221124124310441

偏相关系数

在多要素所构成的系统中，当研究某一个要素对另一个要素的影响或相关程度时，把其他要素的影响视作常数（保持不变），即暂时不考虑其他要素影响，单独研究两个要素之间的相互关系的密切程度，所得数值结果为偏相关系数

• 计算偏相关系数并绘图

  library(corpcor)
  cor2pcor(R) # 计算得到偏相关阵
  library(corrplot)
  corrplot(cor2pcor(R), method="color", addCoef.col='grey', tl.col='black') # 热力图

  

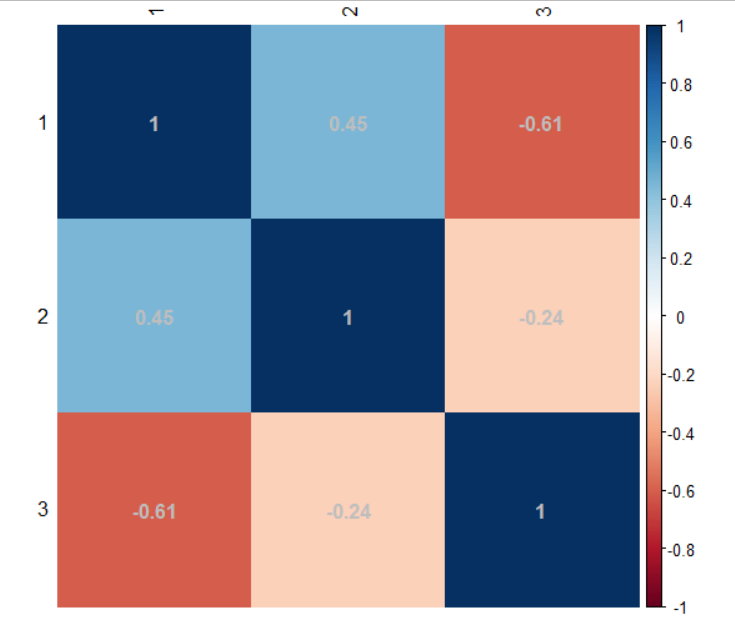
  偏相关系数图

建立模型

• 最小二乘回归

  model <- lm(y~x1+x2+x3+x4+x5, data)     # 最小二乘回归
  #model <- lm(y~0+x1+x2+x3+x4+x5, data)   # 无截距项最小二乘回归
  fitted(model)                           # 拟合值
  model$coefficients                      # 回归系数
  model$residuals                         # 残差

• 计算杠杆值

  hii <- hatvalues(mo)                                # 杠杆值

  

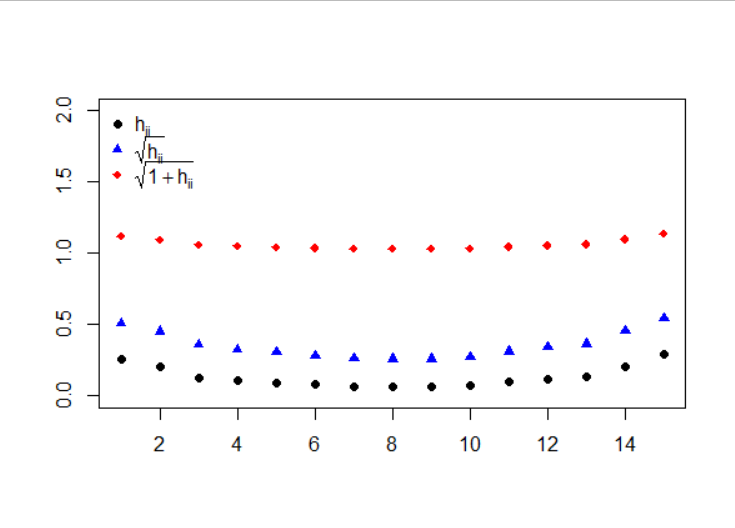
  查看杠杆值(按照X大小顺序排序)
• 计算模型残差

  SSE <- sum(mo$residuals^2)                          # 残差平方和
  sqrt(SSE/(length(data$x)-2))

回归模型检验

• 显著性检验

  summary(model)$r.squared         # R-square
  summary(model)$adj.r.squared     # Adjusted R-square
  sum((result - mean(result))^2)   # SSR
  sum((data$y - result)^2)         # SSE
  sum((data$y - mean(data$y))^2)   # SST, and SST = SSR + SSE
  plot(fitted(model), model$residuals, pch = 19, xlab = "fitted values",ylab = "residuals") # 残差图

  

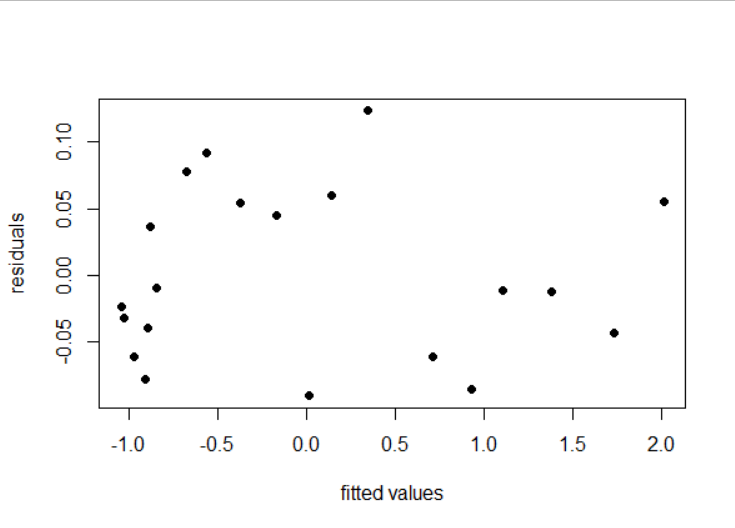
  image-20221124124627132

模型分析

• 点预测

  mo <- lm(y~x,data)                                                  # 最小二乘回归
  none_interval <- predict.lm(mo, data, interval="none")              # 计算点预测值

• 区间预测

  confidence_interval <- predict.lm(mo, data, interval="confidence")  # 计算置信区间预测值
  prediction_interval <- predict.lm(mo, data, interval="prediction")  # 计算预测区间预测值

• 绘制区间图

  # 对齐数据顺序
  data_order <- data[order(data$x),]
  confidence_interval_order <- confidence_interval[order(data$x),]
  prediction_interval_order <- prediction_interval[order(data$x),]

  开始绘图

  plot(data$x, data$y, xlab="x", ylab="y", pch = 16)  # 绘制轮廓
  polygon(c(data_order$x,rev(data_order$x)),c(prediction_interval_order[,2],rev(prediction_interval_order[,3])),col = rgb(221,234,243,max = 255),border = NA)
  polygon(c(data_order$x,rev(data_order$x)),c(confidence_interval_order[,2],rev(confidence_interval_order[,3])),col = "gray",border = NA)  # 其中polygon为绘制多边形的函数，rev为排序函数
  abline(mo, col="red", lwd=2)  
  points(data$x, data$y, pch = 16) 

  

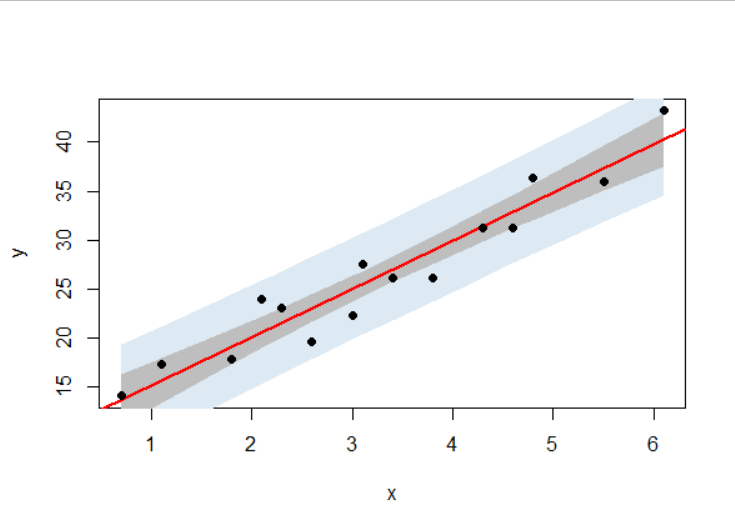
  置信区间和预测区间

预测相关

• 新值预测

  new <- data.frame(x = 3.5)  # 生成新的数据
  predict.lm(mo, new, interval="prediction")  # 点预测+预测上下界
  predict.lm(mo, new, interval="confidence")  # 点预测+置信上下界